题目:
移动距离
X星球居民小区的楼房全是一样的,并且按矩阵样式排列。其楼房的编号为1,2,3...
当排满一行时,从下一行相邻的楼往反方向排号。
比如:当小区排号宽度为6时,开始情形如下:
当排满一行时,从下一行相邻的楼往反方向排号。
比如:当小区排号宽度为6时,开始情形如下:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 12 | 11 | 10 | 9 | 8 | 7 |
| 13 | 14 | 15 | 16 | 17 | 18 |
19
...
...
...
输入为3个整数w m n,空格分开,都在1到10000范围内我们的问题是:已知了两个楼号m和n,需要求出它们之间的最短移动距离(不能斜线方向移动)
w为排号宽度,m,n为待计算的楼号。
要求输出一个整数,表示m n 两楼间最短移动距离。
例如:
用户输入:
6 8 2
则,程序应该输出:
4
再例如:
用户输入:
4 7 20
则,程序应该输出:
5
思路:
其实题目的意思不难理解,就是求出2个数之间的最小距离。可是这并不是一个二维数组,而是一个经过变形了的二维数组。
楼主一开始的思路是:先建立一个标准的二维数组,然后按照题目的要求变形为“X星球居民小区的楼号分布”
按照题目所给的2个楼号找出对应的数组下标,再求最短距离。(楼主语言表达能力不强=.=,看不懂的看下面的流程图吧)
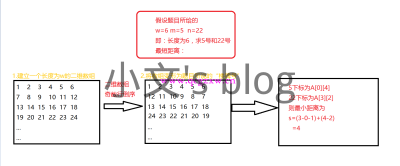
这种方法做出来是完全没有问题的,但是楼主又想到一个好方法
既然楼牌号是固定的,只和w的值有关,那我们大可不必创建二维数组,直接求解。
具体思路为:先判断m和n这两楼牌号所在的行((m-1)/w+1 (n-1)/w+1),
若行差为偶数则说明m n所在的行 同为顺序或者倒序,此时按照同顺序的方式求;
若行差为奇数数则说明m n所在的行 一个为顺序一个为倒序,此时按照不同顺序的方式求;
这样做不仅节约空间,时间复杂度也低。具体步骤看下面流程图
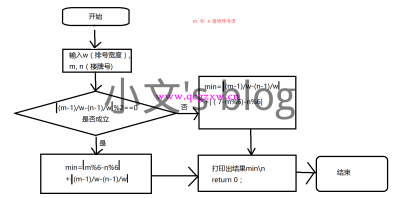
画图累死了0.0,还有几张图由于今天换站点搞的不能显示了,真是悲催,不懂的或者找不到图片的问我吧。
心累求打赏
运行截图:
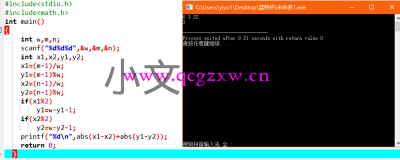
完整代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
#include #include int main() { int w,m,n; scanf("%d%d%d",&w,&m,&n); int x1,x2,y1,y2; x1=(m-1)/w; y1=(m-1)%w; x2=(n-1)/w; y2=(n-1)%w; if(x1%2) y1=w-y1-1; if(x2%2) y2=w-y2-1; printf("%d\n",abs(x1-x2)+abs(y1-y2)); return 0; } |
