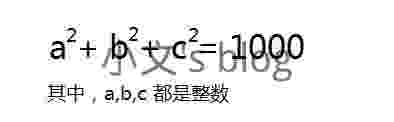题目
方程整数解
方程: a^2 + b^2 + c^2 = 1000
(或参见【图1.jpg】)
这个方程有整数解吗?有:a,b,c=6,8,30 就是一组解。
你能算出另一组合适的解吗?
请填写该解中最小的数字。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
题目分析
- a, b, c分别是是三个什么数
a,b,c是三个整数
整数(integer)就是像-3,-2,-1,0,1,2,3,10等这样的数。
整数的全体构成整数集,整数集是一个数环。在整数系中,零和正整数统称为自然数。-1、-2、-3、…、-n、…(n为非零自然数)为负整数。则正整数、零与负整数构成整数系。整数不包括小数、分数。
- a, b, c的取值范围是多少
31*31=961
32*32=1024
所以a, b, c的取值范围为{-31<=a<=31,-31<=b<=31,-31<=c<=31|a, b, c∈Z}
解题思路
a, b, c 全排列,输出符合条件的abc的值
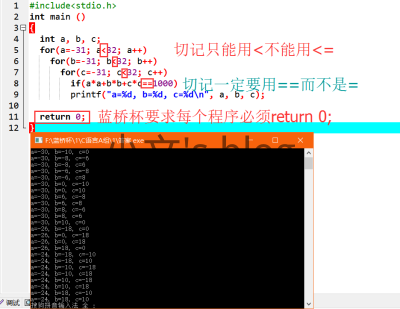
代码示例
|
1 2 3 4 5 6 7 8 9 10 11 12 |
#include<stdio.h> int main () { int a, b, c; for(a=-31; a<32; a++) for(b=-31; b<32; b++) for(c=-31; c<32; c++) if(a*a+b*b+c*c==1000) printf("a=%d, b=%d, c=%d\n", a, b, c); return 0; } |
运行截图
程序结果
网上大部分的答案都是10, 应该是只考虑了正整数的情况, 也许出题人也只考虑了正整数的情况
但是题目明确说明abc是整数,所以我认为答案是-30